あるようでなかったのでまとめておきます。
目次
調和振動子の古典統計と量子統計の違い

証明については僕のノートをそのまま載せたものなので、汚いですがあしからず。
大まかな流れとしては、
- 分配関数を求める。
- 対数微分をして平均エネルギーを求める
- 温度で微分をして比熱を求める
- 分配関数を利用して、平均、分散を求める。
分散についてはそのまま積分をしようとしても大変です。
なので、分散は平均エネルギーの表式まで持っていくのが一番スマートなやり方として知られています。
古典的調和振動子
最初の分配関数を求めるときに利用したハミルトニアンで振動の中心がずれた表式になっていますが、中心を$a$としても0としても結果は同じです。
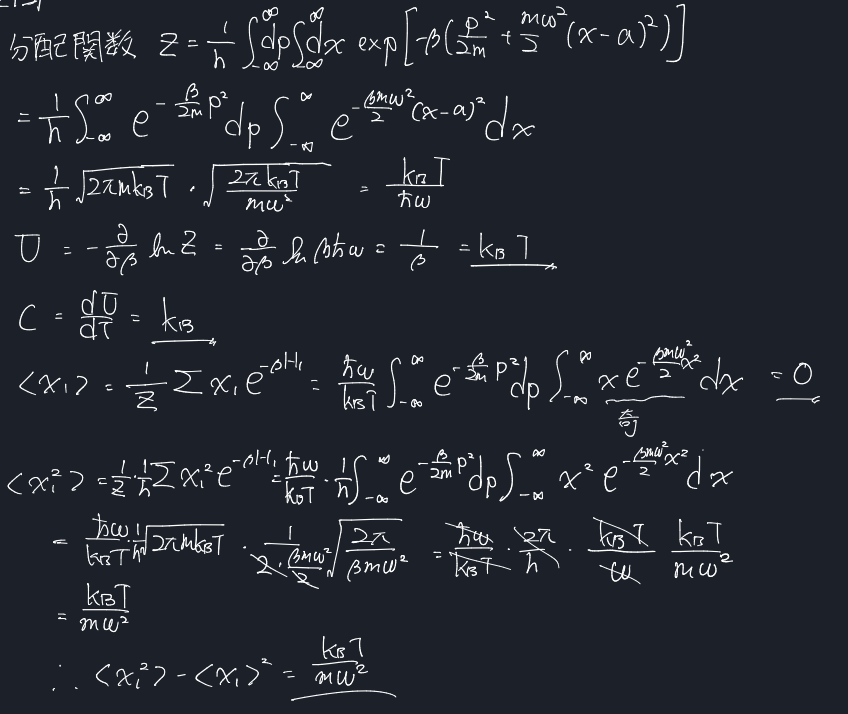
量子的調和振動子

一番下に書いてあるものは気にしないで。関係ないから
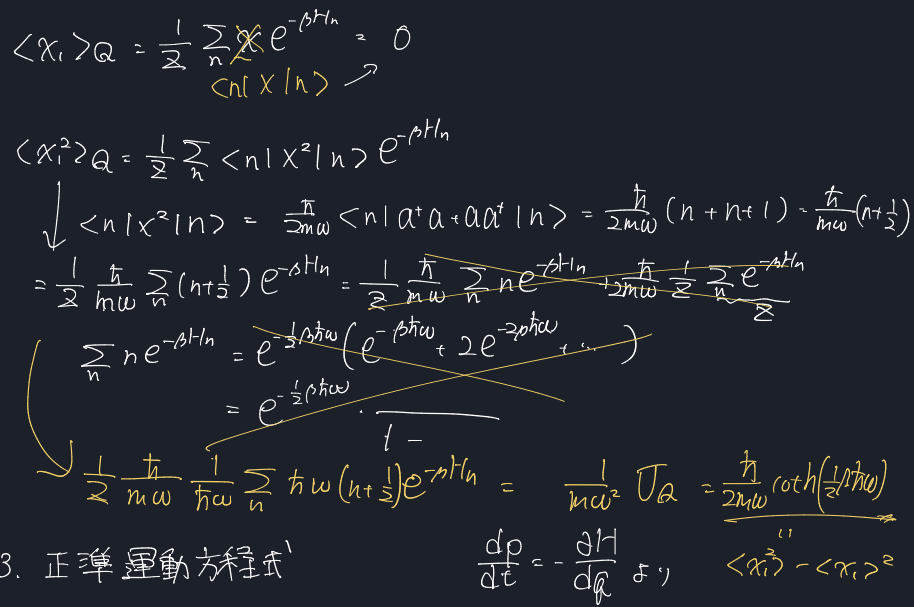


コメント