問題
ポテンシャル
$$V_0(x) = \left\{ \begin{array}
\infty & ( x \leq -L )\\
0 & ( -L < x < L)\\
\infty & (x \geq L )
\end{array} \right.$$
に閉じ込められた質量$m$の粒子の運動を波動関数とエネルギー固有値について考える。
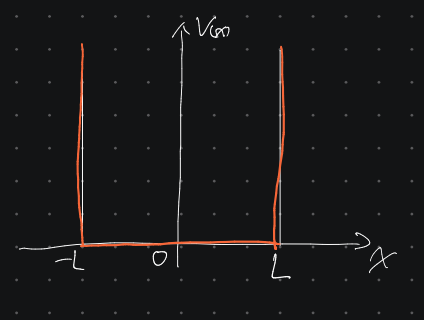
波動関数とエネルギー固有値

今回、ポテンシャルの壁は$\infty$ (正) に取られているので、エネルギー固有値は$E \geq 0$となる。
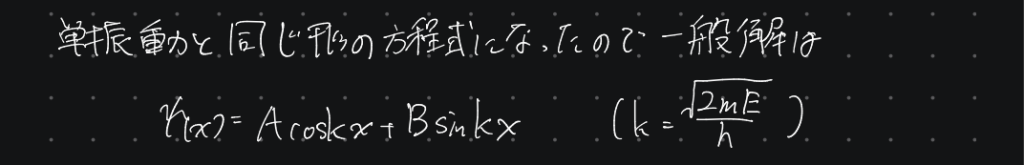
単振動の型の微分方程式の一般解はときに複素数を含んだ指数関数の形で書かれる事がある。
今回は複素数を含めてもメリットはないので三角関数で一般解を表している。
どちらも実部は変わらないため、答えは同じである。

$n$を0からではなく、1から始めた理由は上の波動関数を見てもらえばわかります。
0が当てはまるとしたら偶数の方、つまりsinの方ですが、$x = 0 $としてしまうと$\psi = 0$となり、物理的には粒子さえ存在していないことになってしまうため、$n=0$は考える必要はないのです。

エネルギー固有値は
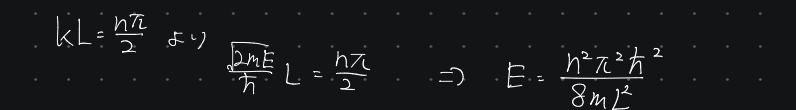
エネルギー固有値の最小の値は$n=1$のときの値となりますが、これは粒子はエネルギーが0にならないということです。エネルギーが最小でもゼロにならないこの現象は零点振動なんて呼ばれています。
これこそが古典論と量子論の大きな違いです。(古典論では当然、最小のエネルギーは0です)
これは不確定性原理でも説明でき、粒子はある区間に閉じ込められているので運動量も有限の値を持たざるを得ないのです。

コメント