20世紀最大の発明と呼ばれることもあるトランジスタ。
今までの僕の知識では、半導体で作られた電子回路の素子という漠然とした知識しかなかったので整理しておく。
トランジスタとは
トランジスタは主に2つのことが行える。
- 電気信号の増幅
- 電気のON/OFFを切り替えるスイッチ
トランジスタは今や集積回路の主役であり、現代のCPUには数十億個ものトランジスタが使われているらしい。そんなに使って色々と大丈夫なのかは謎だが、電子回路には欠かせない素子らしい。
ダイオード
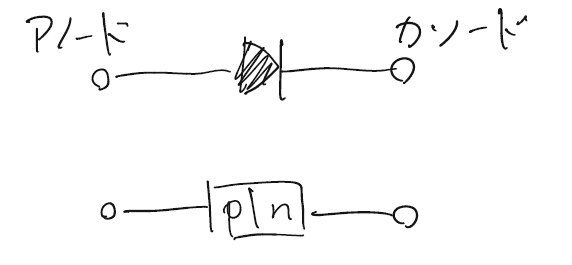
トランジスタの説明をする前にダイオードのついて説明しておく。
ダイオードはp型とn型の半導体をくっつけた素子で、電流を一方向にのみ流すという性質を持つ。
エネルギーバンド図で説明していく。
p型とn型の半導体中の電子と正孔がどのような状態にあるか下の図に示した。
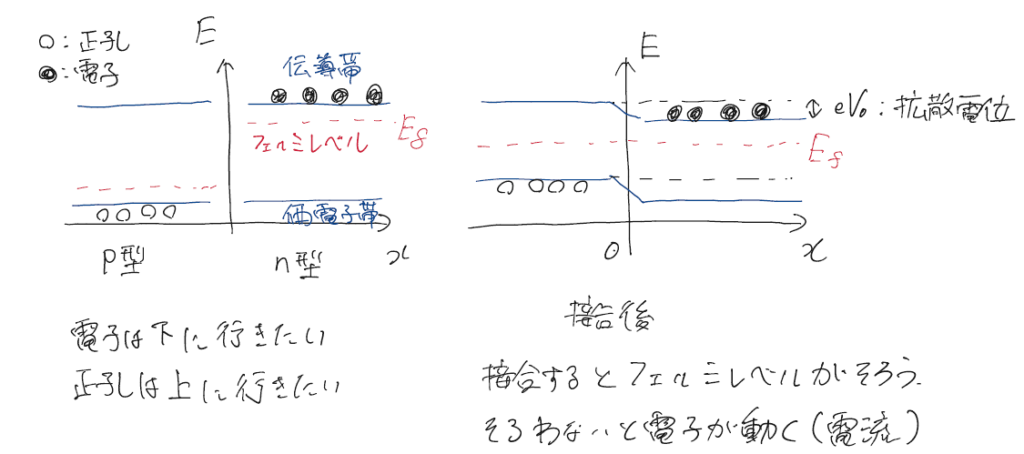
フェルミレベルとは電子がだいたいこのこの辺まで詰まっているよというエネルギーレベルである。
ではこの二種類の半導体をくっつけるとフェルミレベルが揃って、段差のあるような形になる。電子も成功も個の段差(拡散電位)のせいで自由に半導体間を行き来することはできない。また、くっつけるとフェルミレベルが揃う理由は、揃っていないと電子がフェルミレベルの低い側に流れる(電流が生じる)からである。
そんなわけで拡散電位の分だけ電圧をかけてあげると、半導体間のカバがなくなり、電子が流れ始めるようになる。このような原理でダイオードが一方向にしか電流を流さない性質を説明することができた。
トランジスタとは
ここで話をトランジスタに移す。トランジスタは主に2つのことが行える。
- 電気信号の増幅
- 電気のON/OFFを切り替えるスイッチ
トランジスタの中でも、最も一般的なのがMOSFETとっ呼ばれるトランジスタである。これはトランジスタに使われる材料と原理を示しており、metal-oxide-semiconductor feild-effect transistor (金属酸化膜半導体電界効果トランジスタ)の略である。
まず、左の図のように接続された半導体を考える。
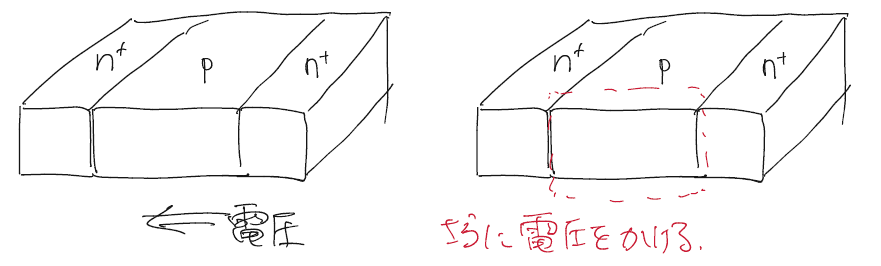
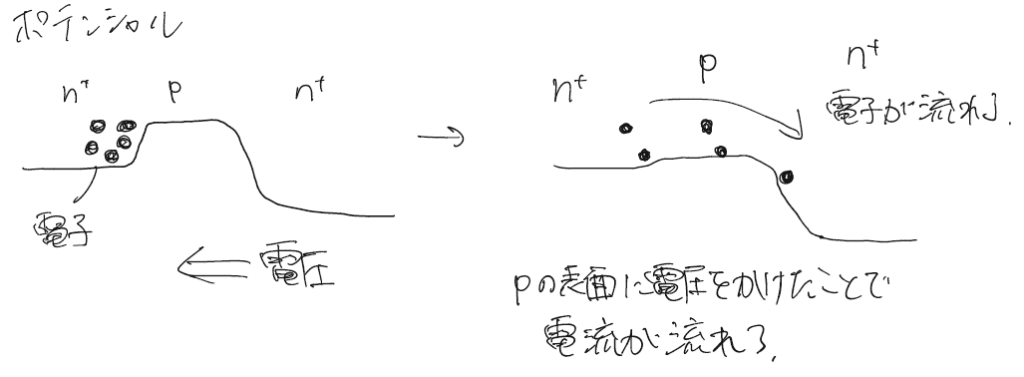
このとき右S側の半導体には電圧がかかっているとする。ここで右の図のようにp型半導体の赤い部分に更に電圧をかけて半導体間の拡散電位による壁をなくすと電流が流れる様になる。このようにしてトランジスタ間を流れる電流を制御することができる。
トランジスタには半導体の接合の仕方によってNMOS、PMOS、CMOSと呼ばれる種類がある。NMOSは今回図で示したもの、PMOSはp型とn型を反転させたもの、CMOSはNMOSとPMOSを組み合わせたものとおぼえておけばとりあえず今は大丈夫である。
電流電圧特性
トランジスタ構造と各部の名称は下図のようになっている。
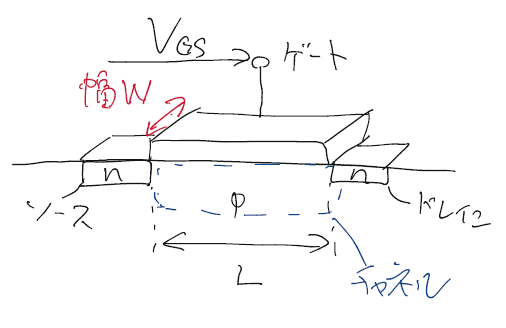
まず、ゲートにのみ電圧を引火した場合を考える。ここでチャネルの電荷密度は\[Q_d = WC_{OX}(V_{GS}-V_{TH})\]となる。$W$はチャネル幅、$CDDD_{OX}$は単位面積あたりの酸化膜容量、$V_{GS}$はソース・ゲート間電圧である。
次にドレインに性の電圧を印加したときは\[Q_d = WC_{OX}(V_{GS}-V(X)-V_{TH})\]となる。ここからは単純な計算をして電流電圧特性を求めていく。
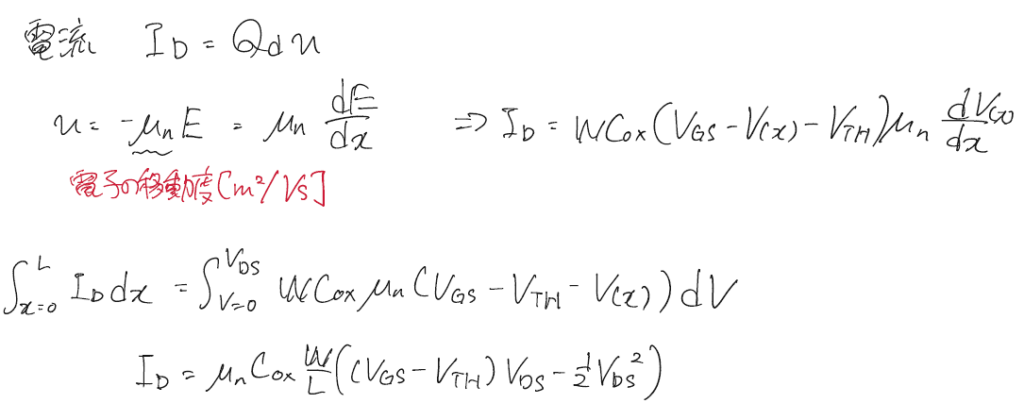
この結果をグラフにすると下図の黒線のようになる。
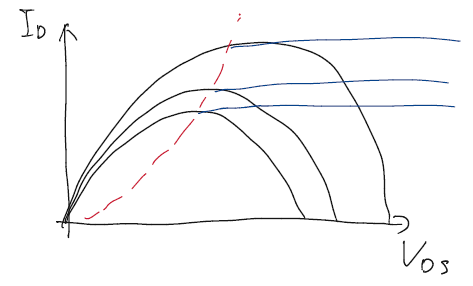
しかし、実際には電圧が大きくなるにつれて電流が落ちるようなことはない(青線)。
つまり、トランジスタは$Q_d=0$を堺に特別な振る舞いを示すわけだがそれはどのようになっているのか。
このときドレイン電圧が高い場合、何が起こっているのかというと、$Q_d$がドレインまで届いていないピンチオフという現象が発生している。
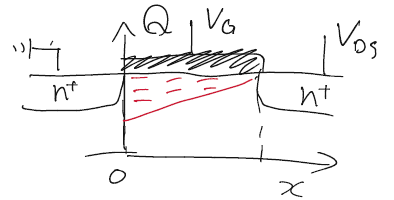
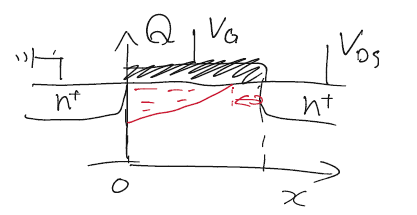
このとき、先程の積分領域は下のように書き換えられ、電流電圧特性も書き換わる。
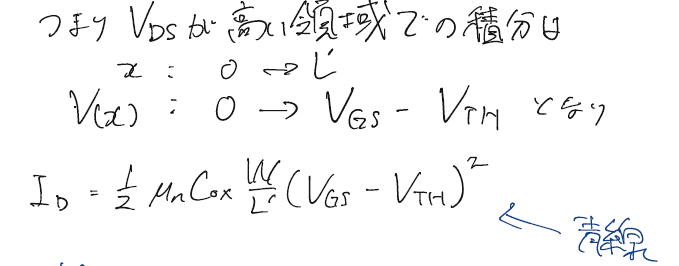
このように電流が一定となる領域(青線)を飽和領域という。それに対し、グラフでの立ち上がりの領域(黒線)を三極管領域とか線形領域という。
線形領域と飽和領域についてまとめると

実際にトランジスタを使う場合は扱いやすい飽和領域で使う場合がほとんどである。
次の記事で詳しく説明するのであまり踏み込まないが下のような回路を考える場合、$V_{in},I_D$の関係は右の図のようになっている。
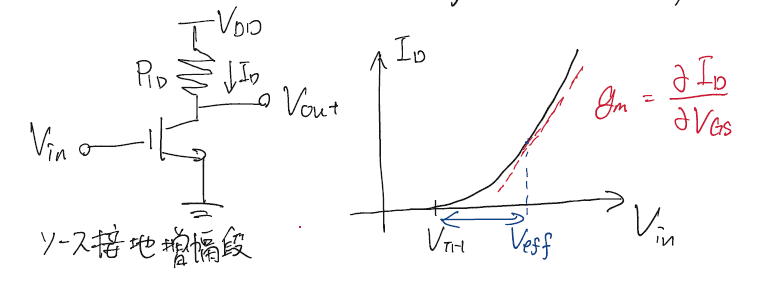
この二次関数でのほとんど一次関数に近似できる領域は抵抗とみなすことができ、トランスコンダクタンス$g_m$という量を定義することができる。トランスコンダクタンスはデバイスが入力電圧の変化量をどれだけ出力電流の変化量に変換するかを示す指標であり、値が大きいほど性能がよいのだ。
トランスコンダクタンスと入力電圧の関係は下の図のようになっている。
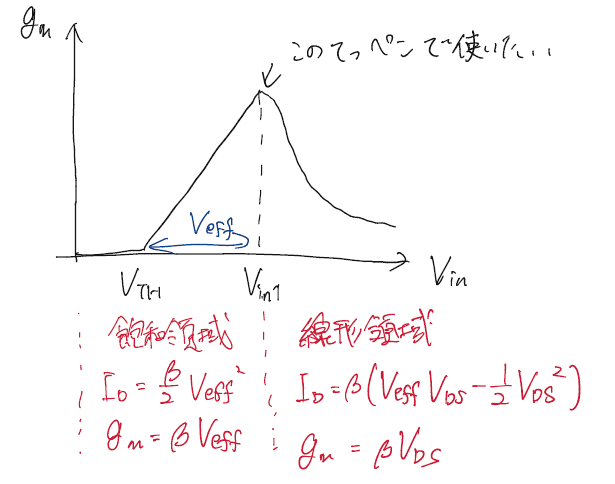
飽和領域と線形領域の中間で最大値を取る。そのため回路を組む際はトランスコンダクタンスが最大となるように設計する。

コメント