今回はガウシアンビーム(ガウスビーム)について解説していく。
ガウシアンビーム
光の広がり方は平面波や球面波がよく知られている。それらの伝搬がよく語られるのは数学的に扱いやすいから、近似的にそれらの光を考えることが多いからという理由にある。ではレーザー光の光はどのような強度分布になっているかというと、それはガウス関数の形をしている。この光のことをガウシアンビームという。
今回はガウシアンビームの導出とその性質を簡単に説明していく。
導出
毎度おなじみのヘルムホルツ方程式から始まる。
\[
\nabla^2 U+k^2 U =0
\]
ビームをz方向に進む波として近似的に考える。(近軸近似)
\[U(\vec{r}) = A(\vec{r}\exp(ikz)\]
ここで近似的にというのは、実際には少し広がりながら進む場合もあるからである。詳しくは後ほどわかる。この式は平面波によく似ているが振幅が$\vec{r}$に対して変化する点が異なる。この式をヘルムホルツ方程式(最初の式)に代入すると
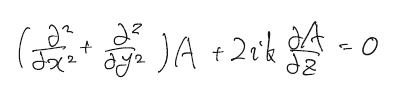
ここで恐ろしいほど天下り的だが、ガウス関数の振幅分布をこのような形で考える。
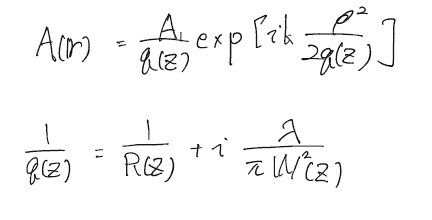
すると
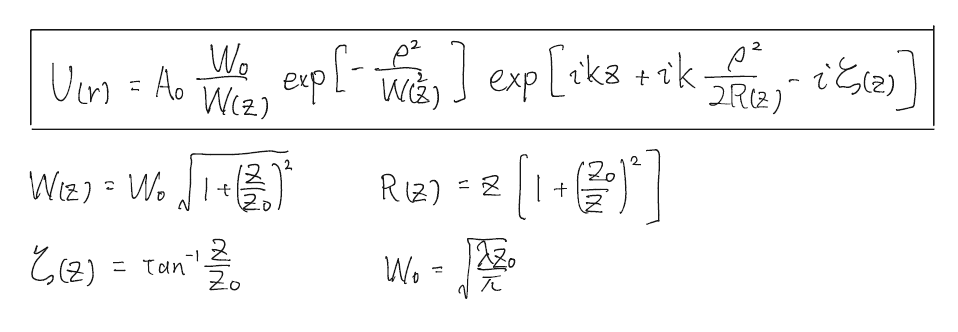
ここまでかなり強引に$U(r)$を求めたが許してほしい。WやRやら意味ありげな形で文字が置かれているので、それらの文字について物理的な意味を説明する。
性質
ガウシアンビームの光強度は以下のようになる。
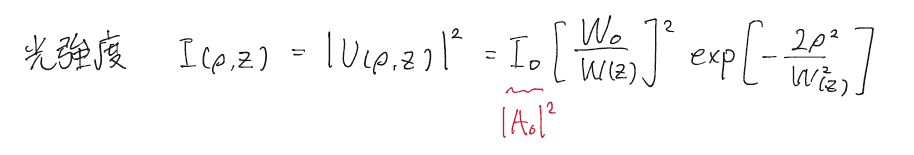
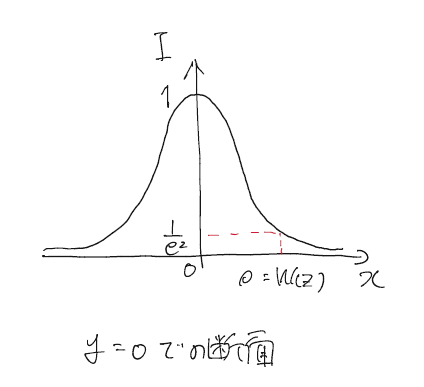
光強度は$\rho=W(x)$で軸上($r=0$)の$1/e^2$まで小さくなる。$W(z)$は各zでのビームの大きさを表している。もっと詳しく書くと
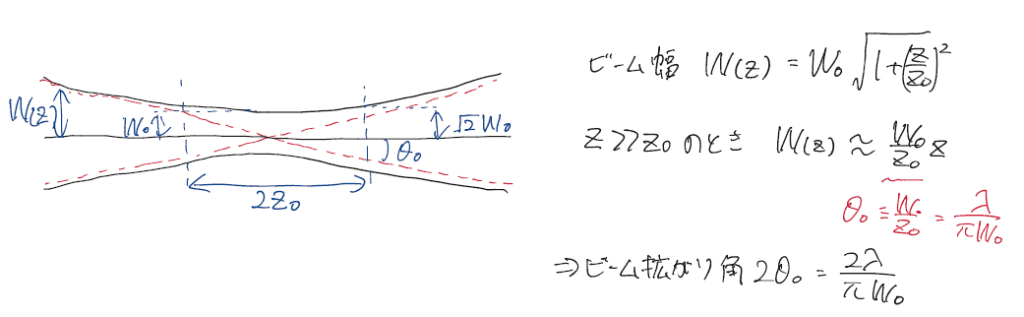
つまりビームの広がりは波長が長いほど大きい、$W_0$が大きいほど小さい。ビームはどう頑張っても広がってしまうので、長く伝搬させるにはレンズで広がったビームを集めつつ伝搬させる必要がある。また$W_0$が大きいほど拡がり角は小さくなるので、ビームを広げて伝搬させれば、途中で挟むレンズの数は少なくなる。
また、$z_0$はレイリー長と呼ばれ、光が絞られている距離を表している。




コメント