私は、ボソン派である。
あなたはどちらでしょう。よかったらコメントで。。。
そんなことはさておき、理想ボース気体について解説していく。
ボース粒子(ボソンについて)
ボソンについて知らない方はこちらの記事で説明している。

理想ボース気体
ここではスピン0の理想ボース気体を考える。体積は十分に大きいとして、単位体積あたりの1粒子状態密度$D(\epsilon)$とボース粒子の分布$f(\epsilon_i)$は以下の式で与えられる。
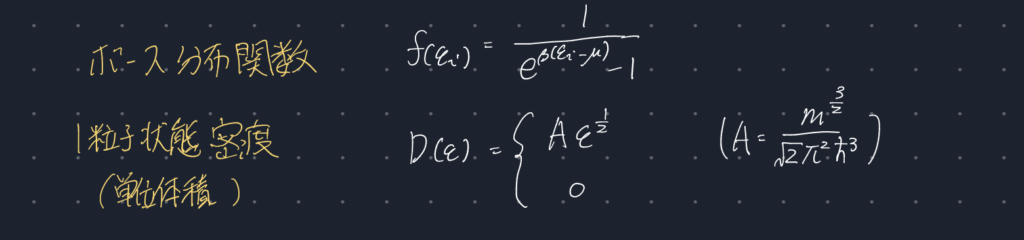
導出は下の記事でしている。

ボース・アインシュタイン凝縮
結論から言うと、ボース系を冷やしていくとある温度より低温になるとボース・アインシュタイン凝縮と呼ばれる現象が起きる。
ボースアインシュタイン凝縮とは、ボース系を極低温にしたとき、ほとんどの粒子が基底状態に落ち込む現象のことである。
では、その温度はどのように決まっているのか。
まあ、粒子によって温度が決められているのだが、粒子の何によって決められているか。
結論から言うと、粒子の質量と密度である。
ボースアインシュタイン凝縮には粒子数密度が関係している。「フェルミオンとボソン」の記事ではボースアインシュタイン凝縮が起きるとき、化学ポテンシャル$\mu$が0にならなければならないという解説をした。
化学ポテンシャル$\mu$が0になるときの温度こそが、凝縮が起きる温度=転移温度$T_C$なのである。
まず、では$\mu = 0 $のときの粒子数密度$\rho$は

この積分はゼータ関数としておいてしまおう。
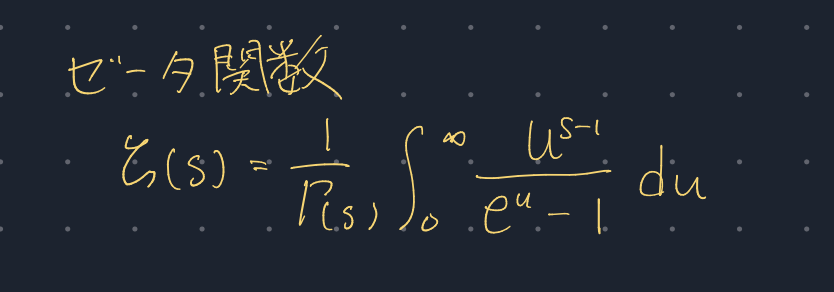
そして、転移温度は量子と古典の境目であるため、転移温度の粒子数密度を古典的な粒子数密度(粒子数を体積で割ったもの)と結びつければ、転移温度が求まる。
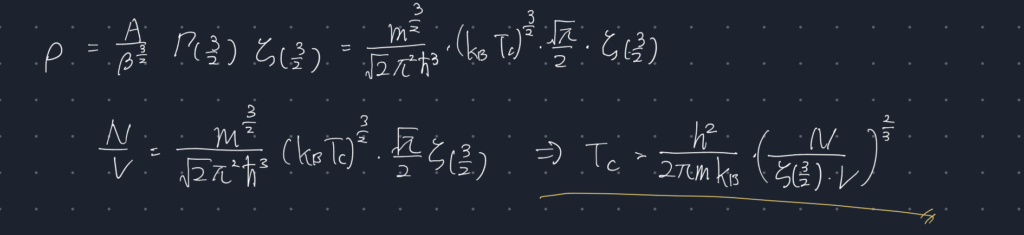
ボース・アインシュタイン凝縮と熱的ド・ブロイ波長
粒子は波としても振る舞うのはご存知のとおりであるが、その波長は系の温度によって変化する。
これは粒子のエネルギーが系の温度の関数であることによるもの。
このように温度によって変化する物質波の波長は熱的ドブロイ波長と呼ばれ、下の式で与えられる。

温度が低いほど熱的ドブロイ波長は長くなる。
そして平均粒子間距離と同程度になったとき、ボースアインシュタイン凝縮が起きるのだ。
余談
物理って、難しい関数を一つの文字でおいてしまって、あたかも簡単なように錯覚してしまうことが多い気がする。その賜物が一般相対性理論だと思うが、それ以外にも球面調和関数とかね。
でも、それを使わないと誰もやる気なんかでなくなるほど、複雑になっちゃうから使わざる負えない。数学者には頭が上がらなないね。今度数学科の友達に飯でも奢ろうかな。数学科の友達なんていなかったわ。トホ、、、




コメント