目次
カノニカル分布・二準位系
一般的な形
POINT
- 比熱はエネルギーゆらぎの２乗に$1/{k_B T^2}$を乗じたもの
- なぜ統計力学では比熱まで求めることが多いのか？
→ 実験で系の性質を見るのには比熱が用いられるから。比熱は「応答係数」とも呼ばれる。
POINT
そもそも比熱って？
→ 比熱は「系の温度をわずかに変えたときエネルギーがどれくらい変化するか」を表す量
二準位系の例
先程のエネルギーを少し書き換えた形を紹介する。
ノート中の計算で比熱は$$C = \frac{\epsilon ^2}{k_B T^2}\frac{1}{(\cosh{\beta \epsilon})^2}$$となった。温度依存のグラフにするとこんな感じ。
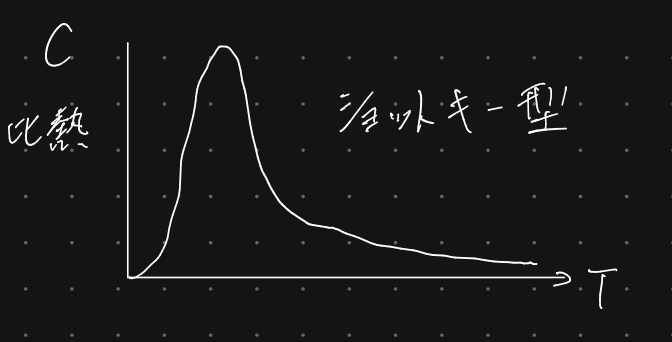
POINT
- 低温 ($k_B T << \epsilon$)
前にある$1/T^2$により発散すると考えられるが、$\cosh{\epsilon/k_BT}$のほうが先に大きな値となるので、低温での比熱は急激に０に近づく - 高温 ($k_B T >> \epsilon$)
$1/T^2$は０に近づき、$\cosh{\epsilon/k_BT}$は１に近づくので高温でも全体として0に近づく
参考文献
田崎晴明 「統計力学〈1〉 (新物理学シリーズ)」[amazon asin=”4563024376″ kw=”統計力学〈1〉 (新物理学シリーズ)”]
コメント