今回は相対論とマクスェル方程式のお話。

目次
問題設定
系$O$において、$z$軸上の$-\infty$から$+\infty$まで一定間隔(間隔$a$)で並べられた荷電粒子(電荷$q$)が、$z$軸にそって速度$\textbf{v}=(0 , 0, v_z)$で等速運動している系Oを考える。
また、荷電粒子と同じ速度で動いている系O’も考える。

電場と磁束密度
それぞれの系での電場と磁束密度はどのようになっているか。
系O:電場

系O:磁束密度

ローレンツ変換
相対論では系Oと系O’との間にはローレンツ変換の関係が成り立つ。
※相対論の教科書ではかなり冒頭に書かれている有名な式である。

すると荷電粒子の間隔$a$は系O’では
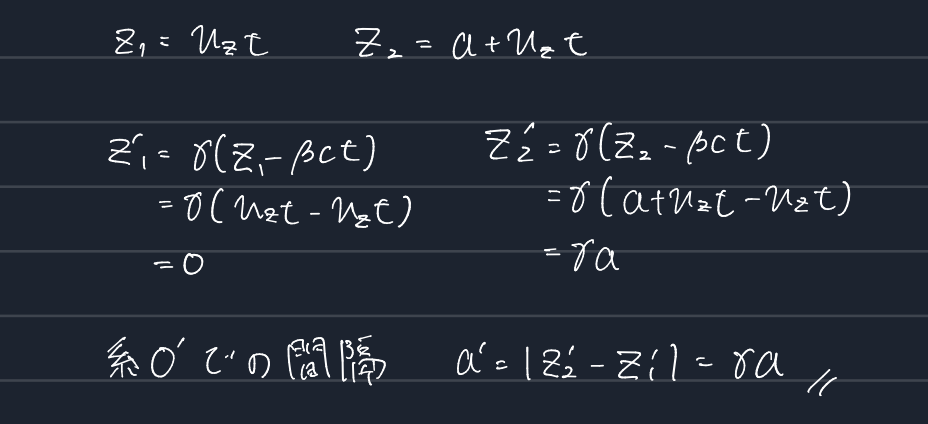
系O’:電場

系O’:磁束密度
荷電粒子は静止して見えるので、磁束密度は$$B’=0$$
電場と磁束密度のローレンツ変換

この変換式に先ほど求めた$\textbf{E’},\textbf{B’}$を入れると
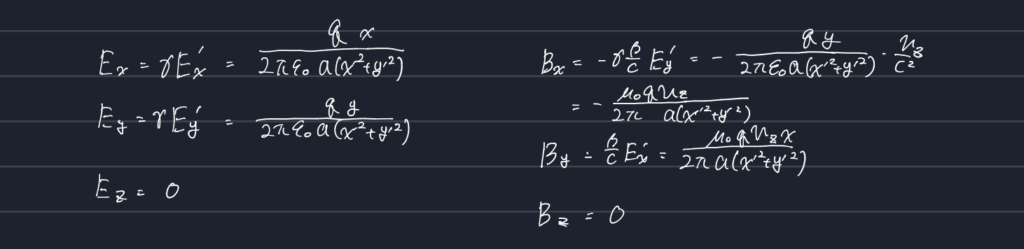
この式において、$(x,0,0)$とすれば、最初に求めた式に戻ることがわかる。
つまり、マクスウェル方程式は相対論を満たす方程式であると言える。
マクスェル方程式ができたのはアインシュタインが相対論を発表する前のことである。
それにも関わらず、相対論を満たしている電磁気学がどれほど進んでいた分野であったか伺える。





コメント