【統計力学】フェルミ粒子とボース粒子

今回はフェルミ粒子とボース粒子について統計力学の立場から解説する。

これらはしばしばフェルミオンやボソンと呼ばれるが意味は同じである。

フェルミオンとボソン

波動関数の違い

この内容は量子力学なので、読み飛ばしてもらっても大丈夫です。

波動関数は以下の対称性を満たす。
フェルミオン：粒子の入れ替えとスピンの反転に対して反対称
ボソン　　　：粒子の入れ替えに対して対称

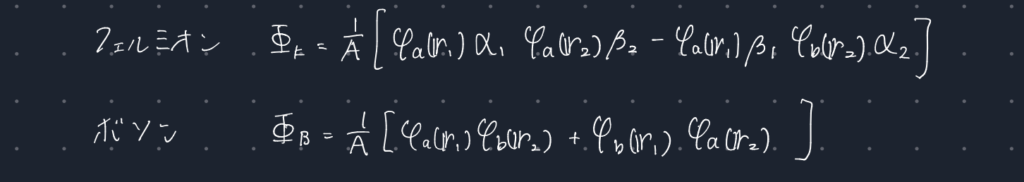
ボソンの波動関数は特に問題はないだろう。
しかし、フェルミオンの波動関数を考えるには工夫が必要になりそうであるが、ある行列式で簡単に表せる。
それはスレーター行列式と呼ばれる行列式で順番通りに波動関数を並べれば良い。

以下が今回のスレーター行列式である。粒子の数に対応して行列式の成分の大きさが増えていくため、例えば４つの粒子を考える場合ならフェルミオンも$\phi_b(\textbf{r})$の軌道も波動関数に入ってくるわけである。

箱の中のフェルミオンとボソン

一辺の長さがLの箱の中のフェルミ気体とボース気体を考える。ここで波動関数は周期的境界条件を満たすものとする。

１粒子の固有状態と固有エネルギー

申し訳ないが、これも量子力学の話である。しかし、ここは統計力学にも必要な知識であるので読み進めてもらいたい。

箱のある辺に対して平行な成分（x成分）のシュレーディンガー方程式からスタート。

状態密度

以上から状態密度を求める。

Lが大きな値であるとすると、$n_x, n_y, n_z$の組み合わせの数Nは球の面積の形で与えることができる。

絶対零度におけるエネルギー

$T=0$の場合におけるN個の粒子系でのエネルギーを計算する。

フェルミ粒子系の場合、低いエネルギー準位から一つずつ粒子が詰まっていく。
そのため、粒子の占めるエネルギーには上限（フェルミエネルギー）が存在する。

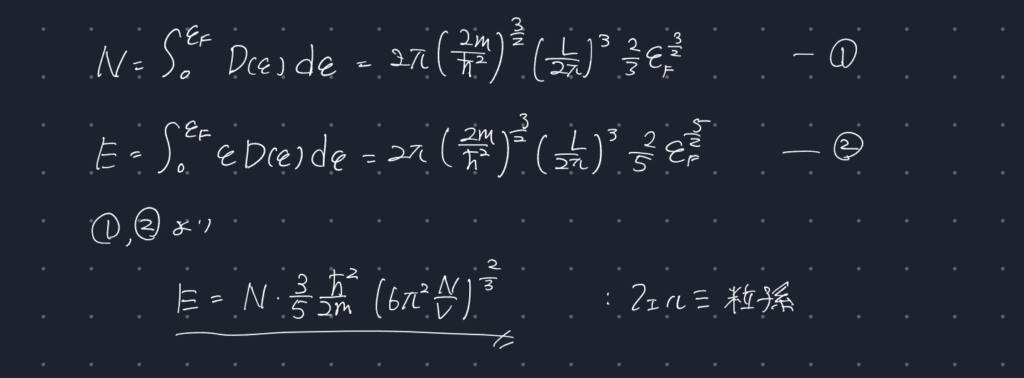
ボース粒子系では、すべての粒子が$E=0$の基底状態に落ち込むため、合計のエネルギーも０である。この現象はボースアインシュタイン凝縮と呼ばれる。

グランドカノニカルアンサンブル

一つの状態に入る粒子数の分布

大分配関数は下のように定義される。

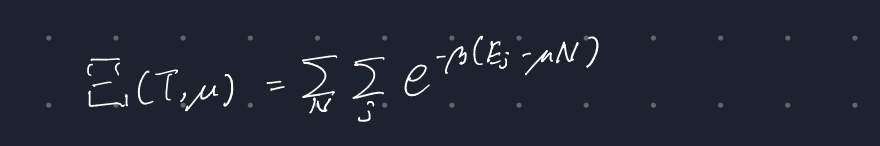
$N$は系の全粒子数、$E_j$は$j$番目のエネルギー準位である。
ここから、粒子数の分布（フェルミ分布、ボース分布）を求めていく。

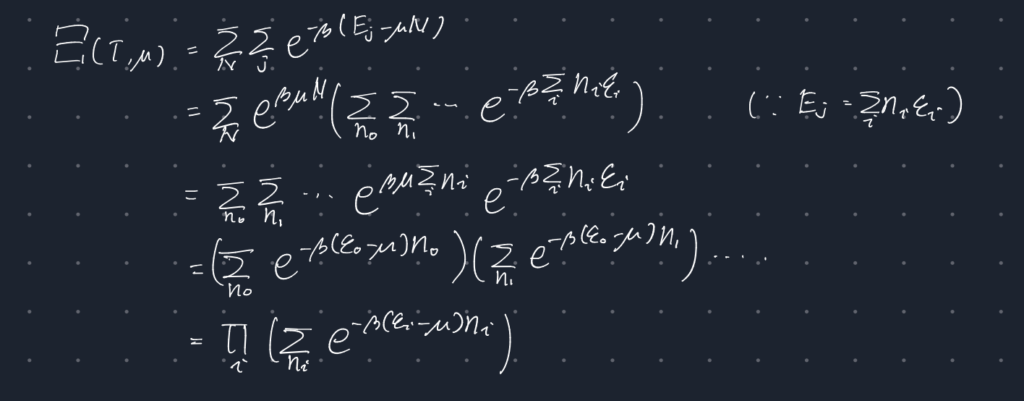
これより先は一つの状態に入れる粒子は一個までのフェルミ粒子系と何個でも入れるボース粒子系では違った振る舞いをします。

なんともきれいな結論ですね。符号が違うだけです。

フェルミ分布をグラフにすると、下のようになります。

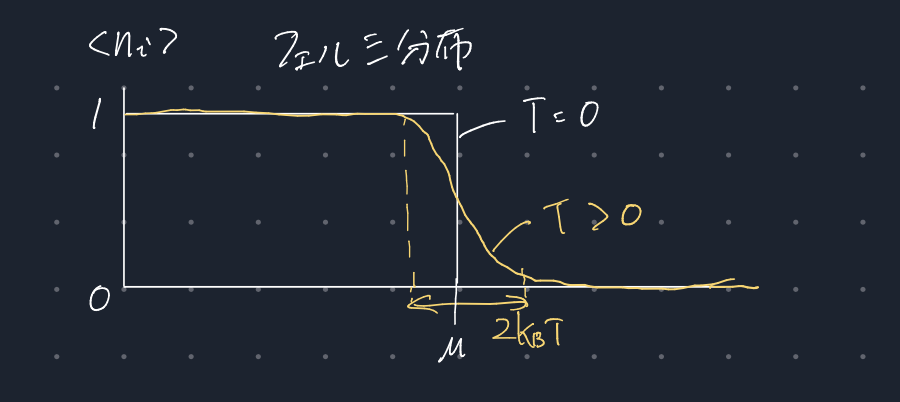
フェルミ分布はTが有限の値を持つとグラフがなまるのが特徴です。

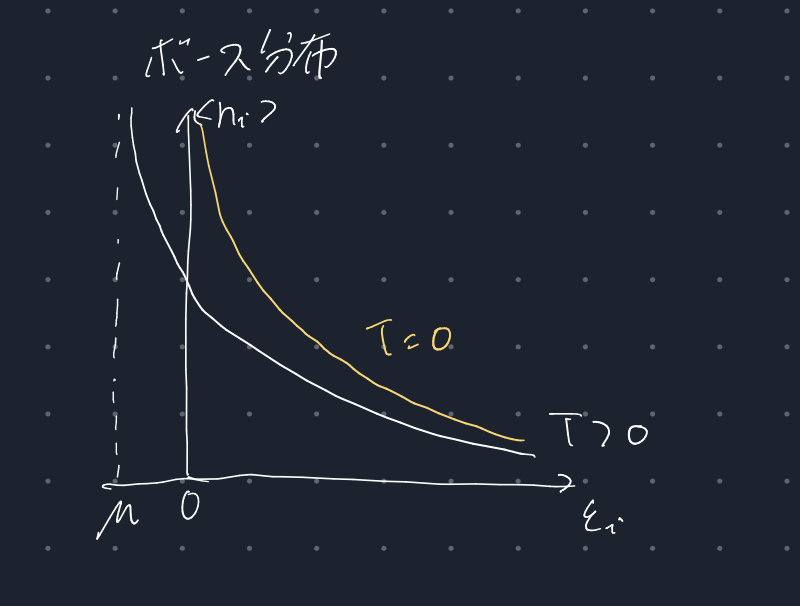
次にボース分布をグラフにしたいのですが、その前に少し議論が必要です。
粒子数の分布であるボース分布が負になることはありません。（粒子数が負などというのはおかしい）
したがって、化学ポテンシャル$\mu$は常に$\mu \leq 0$でなければならないのです。
また、T=0のとき

このことを踏まえてグラフにします。