偏光とはなにか?
光は電磁場の振動であるというのが現代の結論であるが、光の進む向きから光を見るとする。
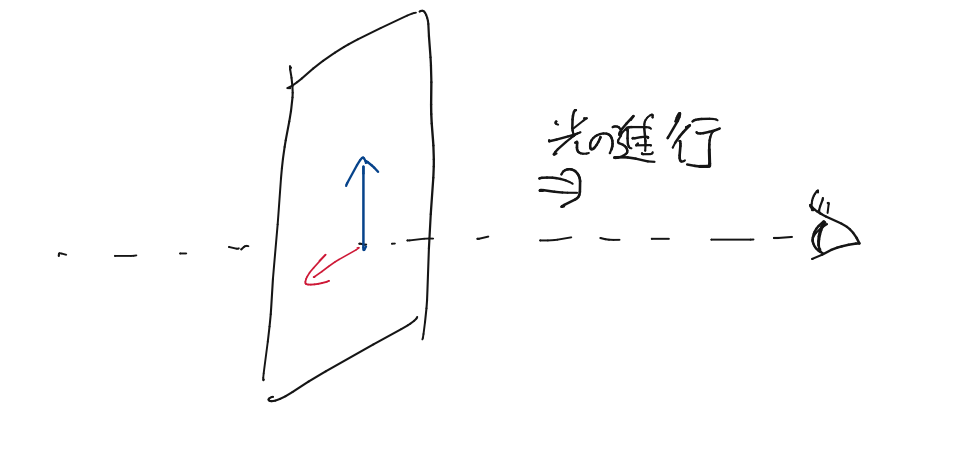
このとき、光の進行に対して僕らの目は青と赤の電磁場の振動がどの割合で混ざっているのかわからない。また、その割合が時間変化しているのかもしれない。生活している中では見ることがない偏光なのだが、物理的に光を語るには重要な概念だったりする。
偏光
偏光とは振動する電場ベクトルの向きである。電場に垂直な磁場を考えても同じように考えることはできるが、物理学者は扱いの簡単な電場ベクトルを選んだのだろう。以下では電場は複素数として表しているが、実際に意味を持つのは実部のみである。

直線偏光
偏光を表すベクトル、偏光ベクトルが下図のように直線内で振動しているときの偏光状態を直線偏光という。
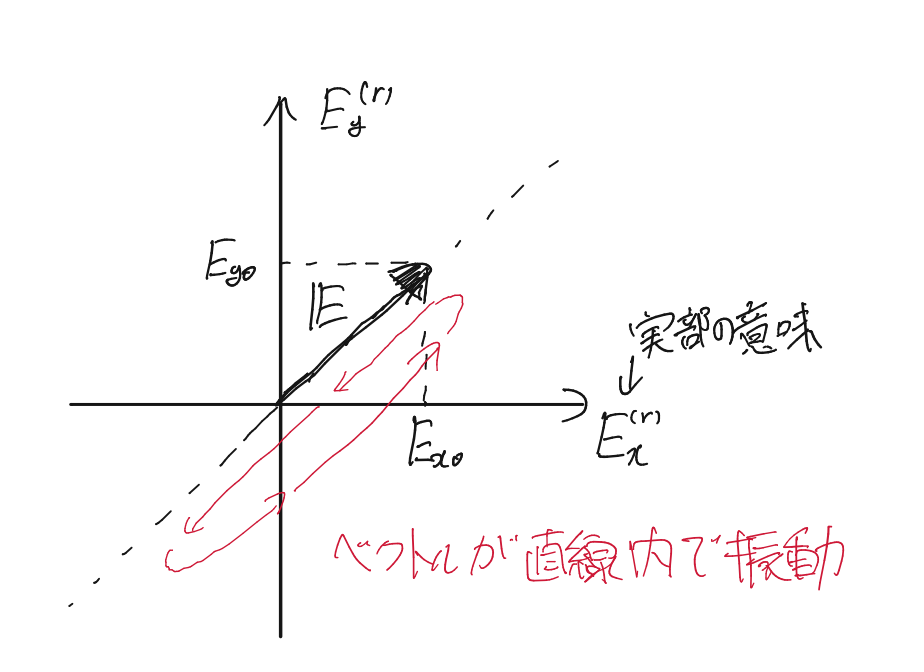
式①の文字で表すと
\[
\delta_x-\delta_y=0 \hspace{5pt}or \hspace{5pt}\pi
\]
のとき直線偏光なのである。このときのベクトルの傾きはそれぞれの成分の大きさの比で決まる。
水面やガラスでの反射光は直線偏光である。この物理を利用して、その偏光成分のみをカットしたものが偏光サングラスや偏光レンズである。
円偏光
偏光ベクトルが下図のように円状に回転しているときの偏光状態を円偏光という。
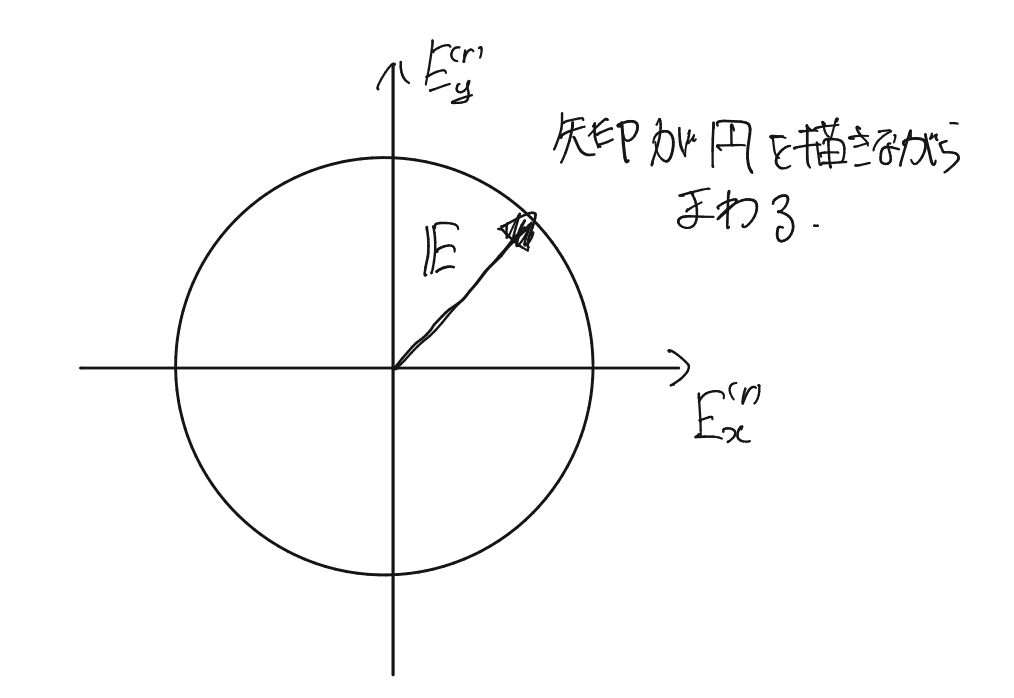
式①の文字で表すと
\[
\delta_x-\delta_y=\pm \frac{\pi}{2} \hspace{10pt}かつ\hspace{10pt} |E_{x0}|=|E_{y0}|
\]
のときが円偏光である。
楕円偏光
偏光ベクトルが下図のよう楕円状に回転しているときの偏光状態を楕円偏光という。
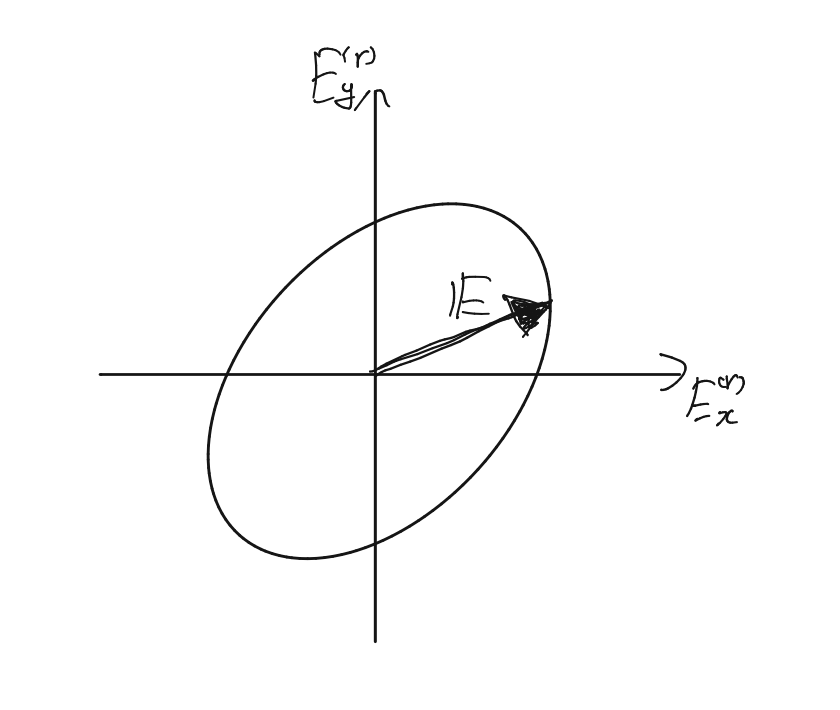
楕円偏光は、直線偏光と円偏光以外の偏光である。
偏光の計算
偏光の行列計算(ジョーンズ行列)
自然界には光の透過後に偏光状態を変化させるような物質がある。このような物質を使って、実験物理学者は偏光を操作するのだ。ここで偏光はベクトルで表せるが、そのときに入射前後の偏光状態を以下のように行列を使って計算する事ができる。
\[\textbf{J}_1=M_J \textbf{J}_0\]
ここで$\textbf{J}_0,\textbf{J}_1$はそれぞれ入射前、入射後の偏光ベクトル(ジョーンズベクトル)を表している。偏光の変化をこのように書いたときの$M_J$をジョーンズ行列という。
例えば、直線偏光を回転させるようなジョーンズ行列は
\[
M_\phi =
\begin{pmatrix}
\cos \phi & -\sin \phi \\
\sin \phi & \cos \phi
\end{pmatrix}
\]
である。これはいわゆる回転行列である。
半波長板
物理学の実験では波長板という偏光状態を操作する板をよく使う(半波長板と1/4波長板が一般的)。
半波長板とはx,y方向のような直交する偏光成分に対し、1/2波長分すなわち$\pi$の位相差をつける素子である。ジョーンズ行列は
\[
\begin{pmatrix}
1 & 0\\
0 & e^{i\pi}
\end{pmatrix}
=
\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}
\]
半波長板に左回りの円偏光を入射すると右回りの円偏光に変換されることが容易にわかる。
1/4波長板
1/4波長分すなわち$\pi/2$の位相差をつける素子を1/4波長板という。ジョーンズ行列は
\[
\begin{pmatrix}
1 & 0\\
0 & e^{i\pi/2}
\end{pmatrix}
=
\begin{pmatrix}
1 & 0\\
0 & i
\end{pmatrix}
\]
1/4波長板の軸に対して45度の角度で直線偏光を入射すると、左回り円偏光になる。
ストークスパラメーター
偏光状態を記述する方法にはもう一つ存在し、ストークスパラメーターというものがある。本質的にはジョーンズベクトルと何ら変わらないものなのだが、ストークスパラメータのほうがポアンカレ球という球の上で議論することができるので、より直感的な表現になる。
ストークスパラメーターは
\begin{align}
S_0 &= I\\
S_1 &= I_{0^\circ}-I_{90^\circ}\\
S_2 &= I_{45^\circ}-I_{-45^\circ}\\
S_3 &= I_{R^\circ}-I_{L^\circ}
\end{align}
ここで、\begin{align}
I &: 全光量\\
I_{0^\circ} &: x偏光成分の光量、I_{90^\circ} : y偏光成分の光量\\
I_{45^\circ} &: 45度偏光成分の光量、I_{-45^\circ} : -45度偏光成分の光量\\
I_{R^\circ}& : 右回り円偏光成分の光量、I_{L^\circ} : 左回り円偏光成分の光量
\end{align}
$S_0=1$となるように規格化すると、$S_1,S_2,S_3$による座標は以下のような三次元球の表面になる。
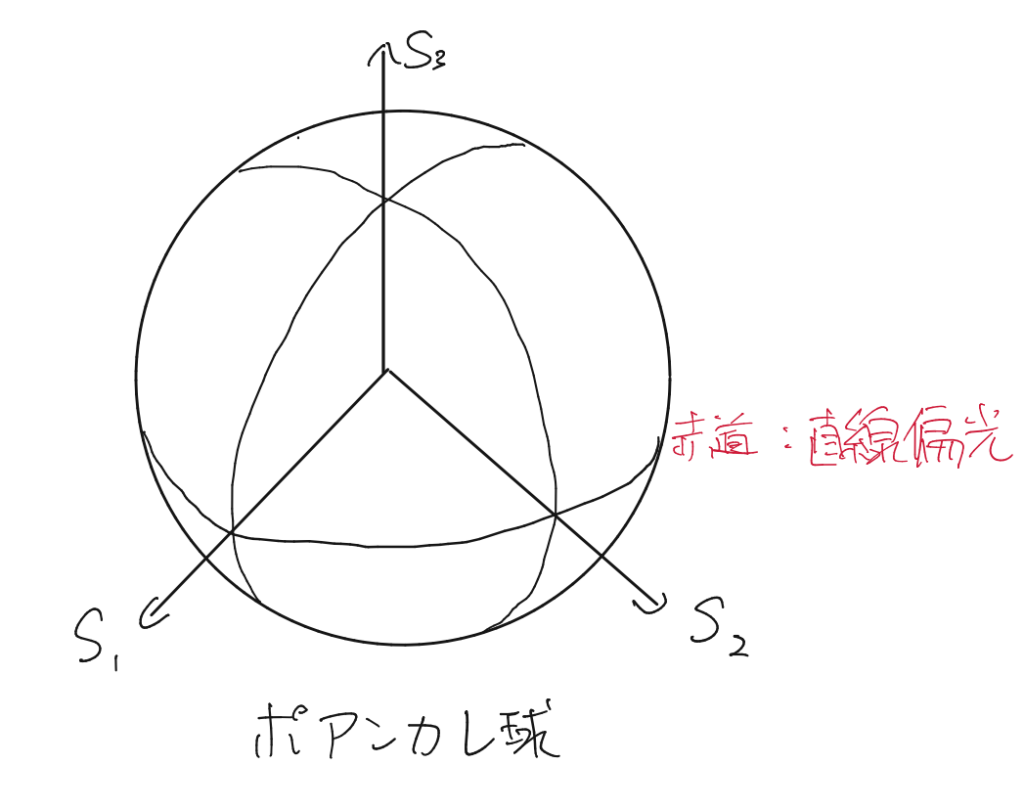
この球をポアンカレ球といい、各座標が偏光の状態を表す。ジョーンズベクトルによる偏光状態の記述より直感的なものになっている。




コメント