光の色で温度を計りたい!!
まずは時代背景から入りましょう。
19世紀後半、製鉄業が急速に発展していました。
製鉄業では溶鉱炉を使うため、高温の物体が光を放射し、温度が高いほど光の波長が短くなることは熱放射として知られていました。
この熱放射の知識で溶鉱炉の温度を炎の色から推定していましたが、製鉄業の発展にともなって溶鉱炉の温度を正確に計りたいという流れになりました。
このような時代背景から、電磁場の熱振動についての研究が急速に進むことになります。
温度ごとの電磁波(光)のスペクトルを調べた
それぞれの温度の光(電磁波)の強度と振動数の相関を調べるためにある実験をしました。
溶鉱炉のように囲まれた空洞を用意し空洞の壁を高温に保つ(下図)。
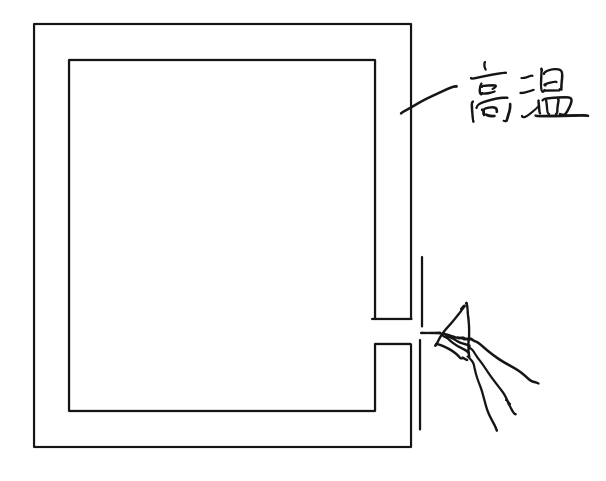
次第に空洞内部の電磁場の熱振動は、壁の温度と平衡状態となる。
そして、空洞に開けられた小さな穴から出る光の強さを振動数$\nu$で分解することにより、温度による電磁波のスペクトル$\rho(\nu)$の変化がわかる。
結構単純な実験ですよね。
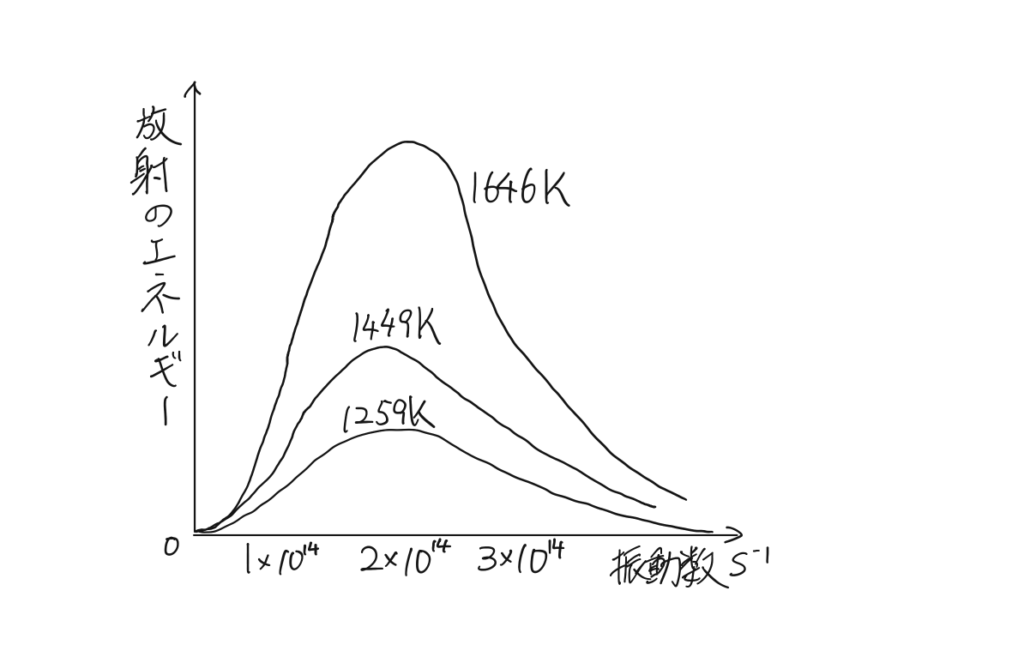
で、実験によって得られた結果が下のグラフです。
プランクの放射式とプランク定数
このグラフについての考察が始まりましたが、うまくこのようなグラフにフィットする式が探し出せませんでした。
そこでプランクがこのグラフに完全にフィットする式を完成させました。
$$\rho(\nu) = a\nu^2 \frac{h\nu}{\exp(\frac{h\nu}{k_BT})-1} プランクの放射式$$
スペクトル図に合うように定数$h$を決めると$h = 6.621676 \times 10^{-34}\rm{J}\cdot \rm{s}$となることがわかりました。
この$h$が量子力学でかなり重要なプランク定数です。
エネルギーの値がとびとびに
さらにプランクの放射式が成り立つ条件を考えていくと、電磁波のエネルギーは連続的なものではなく
$$E = nh\nu (n = 0,1,2,\cdots)$$
になるという結論に至りました。
いままで連続的なものしか扱ってこなかった古典力学では説明の出来ない結論でした。
このように離散的でとびとびの値しか取らない量の単位量「量子」と呼びます。
さて、プランクさんが量子力学の扉を開けました。量子力学の始まりです。






コメント
コメント一覧 (1件)
[…] 【量子力学1-1】プランクの量子仮説【量子力学の誕生!!】ranran-blog.com2020… […]