【光の物理】フレネル回折とフラウンホーファー回折

フーリエ光学、波動光学の最重要部分「回折理論」について説明していきます。

なんで「回折理論」が大事なんでしょうか？
今回導出する式により、光の伝搬のシュミュレーションが行えるようになるからです。

回折理論

ヘルムホルツ方程式（$\Delta^2U+k^2U=0$）を満たす光波
$$U(P)=A(P)\exp[i\phi(P)]$$
を考える。

ここでグリーンの定理
\[\iiint_V(U\Delta^2G-G\Delta^2U)dv=\iint_S\bigg(U\frac{\partial G}{\partial n}-G\frac{\partial U}{\partial n}\bigg)dS \tag{1} \label{a}\]
を導入して、任意の点$\textbf{P}_1$での関数$G$を球面波関数
$$G(P_1)=\frac{\exp(ikr_{01})}{r_{01}}$$
とする。複素関数を学んだ人ならわかると思うが、グリーンの定理を使うには領域$V$の中に特異点を含んではいけない。このため点$P$を中心とする半径$\epsilon$の球面$S_\epsilon$を考え、積分領域からこの球を取り除いた下のような領域を考える。

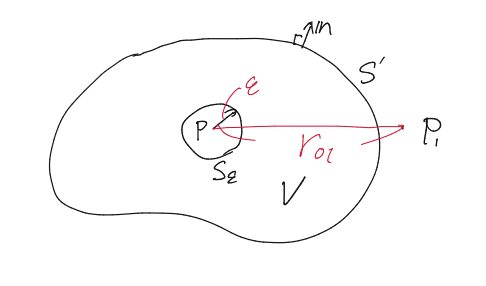
ここまでで関数$U$と$G$が与えられたので、グリーンの定理\eqref{a}の左辺を計算すると０となることが簡単にわかる。
すなわち
\[\iint_S\bigg(U\frac{\partial G}{\partial n}-G\frac{\partial U}{\partial n}\bigg)dS=0\]
$S$は体積$V$を囲むすべての曲面なので$S=S_\epsilon+S’$より
\[-\iint_{S_\epsilon}\bigg(U\frac{\partial G}{\partial n}-G\frac{\partial U}{\partial n}\bigg)dS = \iint_{S’}\bigg(U\frac{\partial G}{\partial n}-G\frac{\partial U}{\partial n}\bigg)dS\]

ここで$\textbf{P}_1$が$S_\epsilon$上にある場合、
\begin{align}
G(P_1)&=\frac{\exp(ik\epsilon)}{\epsilon}\\
\frac{\partial G(P_1)}{\partial n}&=-\frac{\exp(ik\epsilon)}{\epsilon}\bigg(ik-\frac{1}{\epsilon}\bigg)
\end{align}
となるので
\begin{align}
\lim_{\epsilon\to 0} \iint_{S_\epsilon}\bigg(U\frac{\partial G}{\partial n}-G\frac{\partial U}{\partial n}\bigg)dS
&=\lim_{\epsilon\to 0} 4\pi \epsilon^2\bigg[-U(P_0)\frac{\exp(ik\epsilon)}{\epsilon}\bigg(ik-\frac{1}{\epsilon}\bigg)-\frac{\partial U(P_0)}{\partial n}\frac{\exp(ik\epsilon)}{\epsilon}\bigg] \\
&=4\pi U(P_0)
\end{align}
したがって
\[U(P_0)=\frac{1}{4\pi}\iint_{S’}\bigg(G\frac{\partial U}{\partial n}-U\frac{\partial G}{\partial n}\bigg)dS \tag{2} \label{b}\]

この式はヘルムホルツ・キルヒホッフの積分定理という名前の式であり、ある点$P_0$における場はその点を囲む閉曲面の場の情報の積分で表されるということを意味している。
つまりこの式はホイヘンスの原理と同じことを言っており、ホイヘンスの原理を大学物理でより一般的に説明したものであるのだ。

微小開口における光の理論

さらに閉曲面$S’$を下の図のような$S’ = S_1 + S_2$に分離する。

ここで$R\to \infty$とすると[$S_2についての積分=0$]となる。これは無限遠方からの光は届かないという意味である。$S_1$での積分については本来なら壁も含んだ領域の積分も含むが、壁から光は出ていないはずなので$S_1$は開口面を意味するものとする。

すると先ほど示した式\eqref{b}は\[U(P_0)=\frac{1}{4\pi}\iint_{S_1}\bigg(G\frac{\partial U}{\partial n}-U\frac{\partial G}{\partial n}\bigg)dS\]

この式は開口面の情報の合成により、ある点の場は完全に記述されるということを意味している。

話を簡単にするために入射光は平面波であるとする。
\[U=Ae^{iky}\]
開口面での$n$についての偏微分は、$y$についての偏微分と同義であることを利用して各項を計算していく。

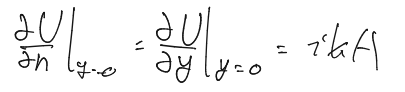
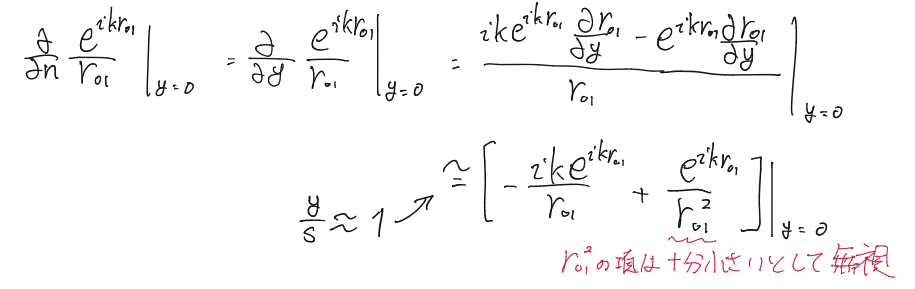
すると
\begin{align}
U(P_0)&=-\frac{ik}{2\pi}\iint_{S_1}U\frac{\exp(ikr_{01})}{r_{01}}dS\\
&\approx \frac{1}{i\lambda r_{01}}\iint_{S_1}Ue^{ikr_{01}}d\xi d\eta
\end{align}
ここで$dS=d\xi d\eta$、開口面内で$r_{01}$はほとんど変化しないとして積分の外に出した。

この式により、開口からの光の回折を計算できるようになった。
しかし、これ以上の近似が扱える場合、式の形はもっと簡単になる。

フレネル近似

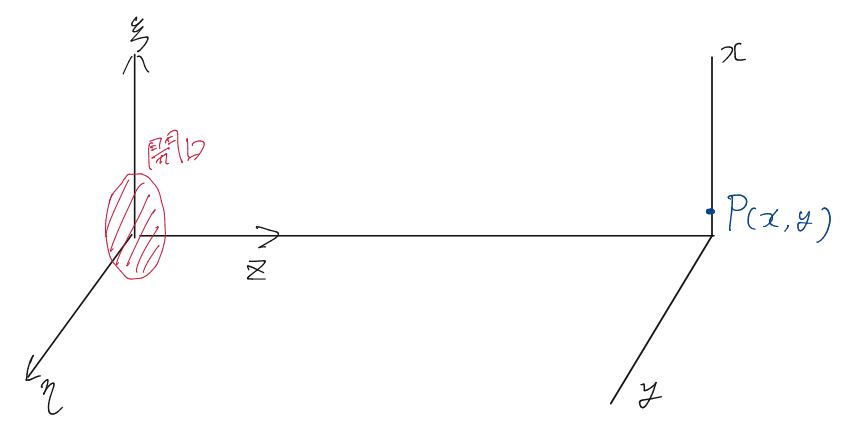
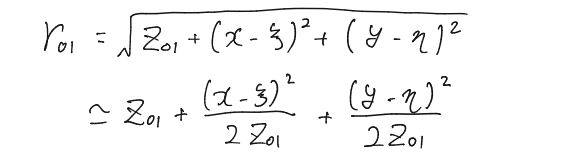
と近似できるとき\begin{align}
U(P_0)&= \frac{1}{i\lambda r_{01}}\iint_{S_1}Ae^{ikr_{01}}d\xi d\eta\\
&\approx \frac{e^{ikx_{01}}}{i\lambda z_{01}}\iint_{S_1}U(\xi,\eta)\exp\bigg(i\frac{k}{2z_{01}}[(x-\xi)^2+(y-\eta)^2]\bigg)d\xi d\eta \end{align}

フレネル近似で得られる回折をフレネル回折という。まあ割りと現実的な距離でフレネル回折が見られるので、いちばん重要だろう。

もっと遠い距離での回折はもっと簡単になる。

フラウンホーファー近似

フレネル近似から、さらに以下のような近似（フラウンホーファー近似）を施す。

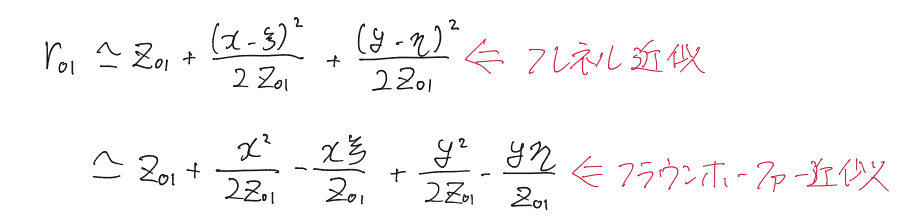
回折式は
\begin{align}
U(P_0)&= \frac{e^{ikz_{01}}}{i\lambda z_{01}}e^{(ik/2z_{01}[x^2+y^2])}\iint_{S_1}U(\xi,\eta)\exp\bigg(-i\frac{k}{z_{01}}[x\xi + y\eta]\bigg)d\xi d\eta
\end{align}

この回折をフラウンホーファー回折という。フラウンホーファー回折像が見られる場所は数km先になったり、少し現実的な距離ではなくなる。しかし、レンズを使えば近い距離でもフラウンホーファー回折像を作り出すことができるのだが、その話はまたいつか。

とにかくここまでの回折理論がフーリエ光学の最重要部分と言っても過言ではない。